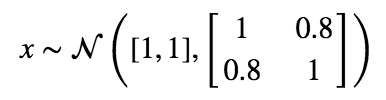While they hit the scene two years ago, Generative Adversarial Networks (GANs) have become the darlings of this year’s NIPS conference. The term “Generative Adversarial” appears 170 times in the conference program. So far I’ve seen talks demonstrating their utility in everything from generating realistic images, predicting and filling in missing video segments, rooms, maps, and objects of various sorts. They are even being applied to the world of high energy particle physics, pushing the state of the art of inference within the language of quantum field theory.
The basic idea is to build two models and to pit them against each other (hence the adversarial part). The generative model takes random inputs and tries to generate output data that “look like” real data. The discriminative model takes as input data from both the generative model and real data and tries to correctly distinguish between them. By updating each model in turn iteratively, we hope to reach an equilibrium where neither the discriminator nor the generator can improve. At this point the generator is doing it’s best to fool the discriminator, and the discriminator is doing it’s best not to be fooled. The result (if everything goes well) is a generative model which, given some random inputs, will output data which appears to be a plausible sample from your dataset (eg cat faces).
As with any concept that I’m trying to wrap my head around, I took a moment to create a toy example of a GAN to try to get a feel for what is going on.
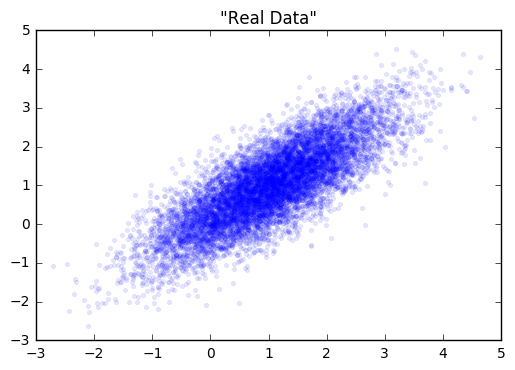
Let’s start with a simple distribution from which to draw our “real” data from.
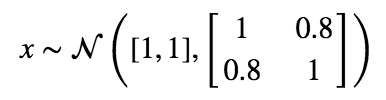
Next, we’ll create our generator and discriminator networks using tensorflow. Each will be a three layer, fully connected network with relu’s in the hidden layers. The loss function for the generative model is -1(loss function of discriminative). This is the adversarial part. The generator does better as the discriminator does worse. I’ve put the code for building this toy example here.
Next, we’ll fit each model in turn. Note in the code that we gave each optimizer a list of variables to update via gradient descent. This is because we don’t want to update the weights of the discriminator while we’re updating the weights of the generator, and visa versa.
loss at step 0: discriminative: 11.650652, generative: -9.347455

loss at step 200: discriminative: 8.815780, generative: -9.117246

loss at step 400: discriminative: 8.826855, generative: -9.462300
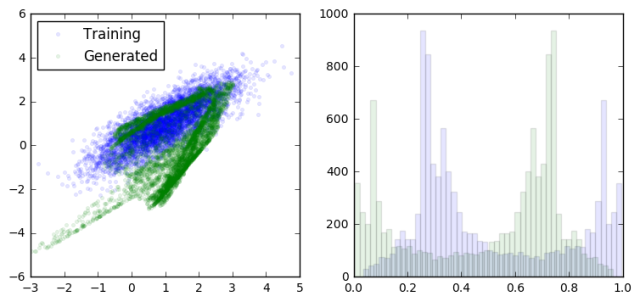
loss at step 600: discriminative: 8.893397, generative: -9.835464

loss at step 3600: discriminative: 6.724183, generative: -13.005814
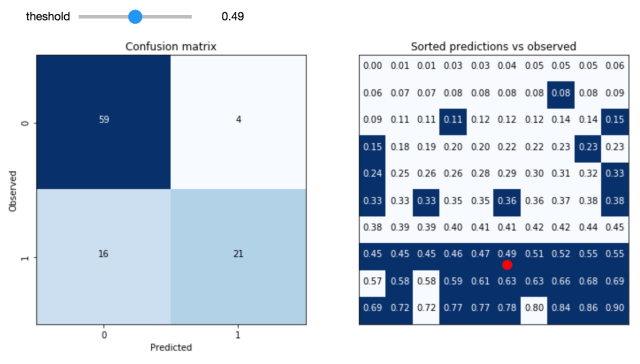
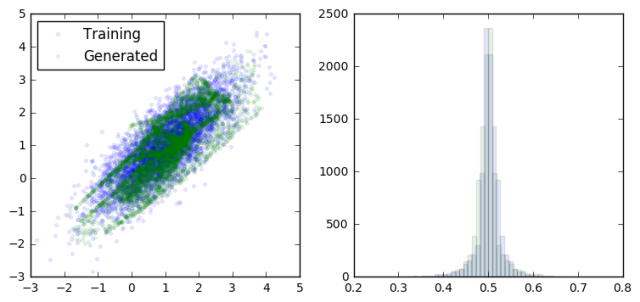
As we can see, the generator is learning to output data that looks more and more like a sample from the training data. At the same time, the discriminator is having a harder and harder dime telling them apart (as seen in the overlapping prediction histograms on the right).
Obviously this is a trivial example to put a GAN to work on, but when it comes to high-dimensional data with complex dependency structures, this approach starts to really shine. I’m sure the hotness of this approach won’t cool off any time soon.