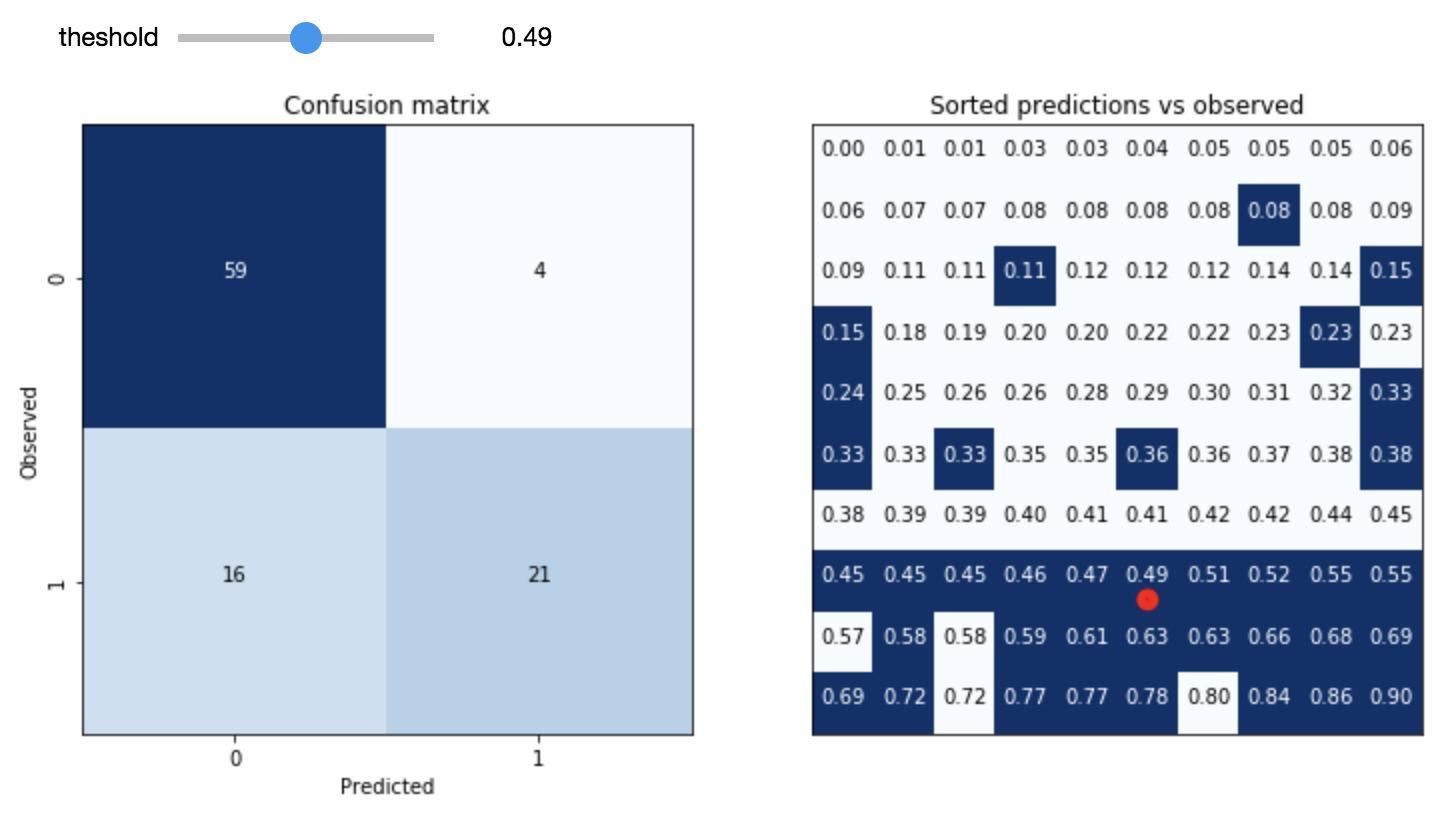
In Magritte’s famous 1929 painting The Treachery of Images, a pipe is depicted with the caption “Ceci n’est pas une pipe“, French for “This is not a pipe”. The seemingly dissonant statement under what is a very clearly depicted pipe forces the viewer to confront the distinction between the representation and the thing itself. The treachery refers to the danger involved in confusing the representation with the object.
Models – like images – are merely representations of the objects they depict. The modeler seeks to represent the relevant properties of the system being modeled in order to communicate some features of that system, or to manipulate it under ‘what-if’ scenarios.
With the current plethora of models of COVID-19 spread, it seems important to remind ourselves of Magritte’s warning. Models can be incredible tools — abstractions of complex realities that allow us to reason about the data we’ve seen so far, and consider possible futures. But they are not the epidemic process itself.

This is not an argument that the models themselves are treacherous. I absolutely adore modeling and models, as Magritte adored painting and images. I consider modeling an essential tool to further our understanding of (and make predictions about) the world around us. Indeed I developed one of the aforementioned COVID-19 models with my colleagues at Penn Medicine. The treachery comes when we mistake the abstraction for reality.