Tag Archives: gambling

The Gambling Machine Puzzle

By Posted in decision making, Probability, Rstats, uncertainty Tagged , , , , 18 Comments

This puzzle came up in the New York Times Number Play blog. It goes like this:

An entrepreneur has devised a gambling machine that chooses two independent random variables x and y that are uniformly and independently distributed between 0 and 100. He plans to tell any customer the value of x and to ask him whether y > x or x > y.

If the customer guesses correctly, he is given y dollars. If x = y, he’s given y/2 dollars. And if he’s wrong about which is larger, he’s given nothing.

The entrepreneur plans to charge his customers $40 for the privilege of playing the game. Would you play?

I figured I’d give it a go.  Since I was feeling lazy, and already had my computer in front of me, I thought that I’d do it via simulation rather than working out the exact maths. I tried playing the game with the first strategy that came to mind. If x<50, I would choose y>x, and if x>50, I’d choose y<x, figuring I’d maximize my probability of winning something rather than nothing. This was probably due to the inherent risk aversion of system one. Let’s see how that works out:

N<-100000
x<-sample.int(100,N,replace=TRUE)
y<-sample.int(100,N,replace=TRUE)
dec_rule=50
payout<-numeric(N)
for(i in 1:N)
{
## Correct Guess (playing simple max p(!0) strategy)
if( (x[i]>dec_rule & y[i]<x[i]) | (x[i]<=dec_rule & y[i]>x[i]) )
payout[i]<-y[i]

## Incorrect Guess (playing simple max p(!0) strategy)
if( (x[i]>dec_rule & y[i]>x[i]) | (x[i]<=dec_rule & y[i]<x[i]) )
payout[i]<-0

## Tie pays out y/2
if(x[i] == y[i])
payout[i]<-y[i]/2
}
## Expected Payout ##
print(paste(dec_rule,mean(payout)))

Which leads to an expected payout of $37.75. Playing the risk averse strategy leads to an expected value less than the cost of admission, loosing on average 25 cents per play. No deal, Mr entrepreneur, I had something else in mind for my forty bucks anyway.

Lets try alternate strategies, and see if we can’t play in such a way as to improve our outlook.

## Gambling Machine Puzzle ##
## Puzzle presented in http://wordplay.blogs.nytimes.com/2013/03/04/machine/

result<-numeric(100)
for(dec_rule in 1:100)
{
N<-10000
x<-sample.int(100,N,replace=TRUE)
y<-sample.int(100,N,replace=TRUE)

payout<-numeric(N)

for(i in 1:N)
{
## Correct Guess (playing dec_rule strategy)
if( (x[i]>dec_rule & y[i]<x[i]) | (x[i]<=dec_rule & y[i]>x[i]) )
payout[i]<-y[i]

## Incorrect Guess (playing dec_rule strategy)
if( (x[i]>dec_rule & y[i]>x[i]) | (x[i]<=dec_rule & y[i]<x[i]) )
payout[i]<-0

## Tie pays out y/2
if(x[i] == y[i])
payout[i]<-y[i]/2
}

## Expected Payout ##
print(paste(dec_rule,mean(payout)))
result[dec_rule]<-mean(payout)
}
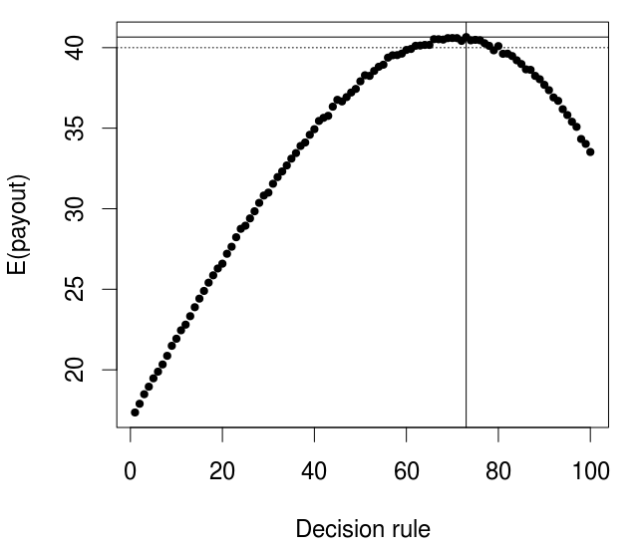
par(cex=1.5)
plot(result,xlab='Decision rule',ylab='E(payout)',pch=20)

abline(v=which.max(result))
abline(h=max(result))
abline(h=40,lty=3)

gmachine

According to which, the best case scenario is an expected payout of $40.66, or an expected net of 66 cents per bet, if you were to play the strategy of choosing y>x for any x<73 and y<x for any x>73. You’re on, Mr entrepreneur!

To calculate the exactly optimal strategy and expected payout, we would need to compute the derivative of the expected payout function with respect to the within game decision threshold. I leave this fun stuff to the reader 😉

Did the sun just explode? The last Dutch Book you’ll ever make

By Posted in Probability, Rstats Tagged , , , , , , , , , 11 Comments

In today’s XKCD, a pair of (presumably) physicists are told by their neutrino detector that the sun has gone nova. Problem is, the machine rolls two dice and if they both come up six it lies, otherwise it tells the truth.

The Frequentist reasons that the probability of obtaining this result if the sun had not, infact, gone nova is 1/36 (0.027, p<0.05) and concludes that the sun is exploding. Goodbye cruel world.

The Bayesian sees things a little differently, and bets the Frequentist $50 that he is wrong.

Let’s set aside the obvious supremacy of the Bayesian’s position due to the fact that were he to turn out to be wrong, come the fast approaching sun-up-to-end-all-sun-ups, he would have very little use for that fifty bucks anyway.

What prior probability would we have to ascribe to the sun succumbing to cataclysmic nuclear explosion on any given night in order to take the Bayesian’s bet?

Not surprisingly, we’ll need to use Bayes!

P(S|M) = \frac{P(M|S)P(S)}{P(M|S)P(S)+P(M|S \urcorner)P(S \urcorner)}

Where M is the machine reading a solar explosion and S is the event of an actual solar explosion.

Assuming we are risk neutral, and we take any bet with an expected value greater than the cost, we will take the Bayesian’s bet if P(S|M)>0.5. At this cutoff, the expected value is 0.5*0+0.5*100=50 and hence the bet is worth at least the cost of entry.

The rub is that this value depends on our prior. That is, the prior probability that we ascribe to global annihilation by complete solar nuclear fusion. We can set P(S|M)=0.5 and solve for P(S) to get the threshold value for a prior that would make the bet a good one (ie not a Dutch book). This turns out to be:

P(S) = 1-\frac{P(M|S \urcorner)}{P(M|S)P(M|S \urcorner)}, where P(S|M) = 0.5

Which is ~0.0277 — the Frequentist’s p-value!

So, assuming 1:1 payout odds on the bet, we should only take it if we already thought that there was at least a 2.7% chance that the sun would explode, before even asking the neutrino detector. From this, we can also see what odds we would be willing to take on the bet for any level of prior belief about the end of the world.

sun_explode<-function(P_S)
{
P_MgS<-35/36
P_MgNS<-1/36
P_NS<-1-P_S

P_SgM<-(P_MgS*P_S)/(P_MgS*P_S + P_MgNS*P_NS)

return(P_SgM)
}

par(cex=1.3,lwd=2,mar=c(5,5,1,2))
curve(sun_explode(x),
xlim=c(0,0.1),
ylab='P(Sun Exploded | Neutrino Machine = YES)',
xlab='P(Sun Exploded) - aka your prior')

text(0.018,0.2,'No\n thanks')
text(0.07,0.6,'A good bet,\n but frightful existence')

abline(h=0.5,lty=2)
abline(v=0.0277,lty=2)