Category Archives: Probability

Visualising the Metropolis-Hastings algorithm

By Posted in Probability, Rstats, Uncategorized 6 Comments

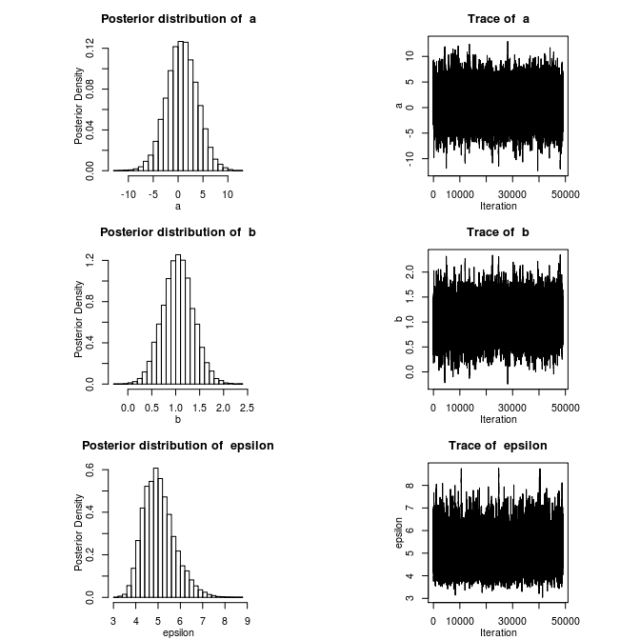
In a previous post, I demonstrated how to use my R package MHadapive to do general MCMC to estimate Bayesian models. The functions in this package are an implementation of  the Metropolis-Hastings algorithm. In this post, I want to provide an intuitive way to picture what is going on ‘under the hood’ in this algorithm.

The main idea is to draw samples from a distribution which you can evaluate at any point, but not necessarily  integrate (or at least, you don’t want to). The reason that integration is important come from Bayes theorem itself:

P(θ|D)=P(D|θ)P(θ)/P(D)

Where P(D) is the unconditional probability of observing the data. Since this is not dependant on the parameters of the model (θ) on which we wish to perform inference, P(D) is effectively a normalising constant which makes P(θ|D) a proper probability density function (ie. integrates to 1).

So, we have a non-normalised probability density function which we wish to estimate by taking random samples. The process of taking random samples itself is often difficult for complex models, so instead we explore the distribution using a Markov chain. We need a chain which, if run long enough, will consist as a whole of random samples from our distribution of interest (lets call that distribution π). This property of the Markov chain we are constructing is called ergodicity. The Metropolis-Hastings algorithm is a way to construct such a chain.

It works like this:

  1. Choose some starting point in the parameter space k_X
  2. Choose a candidate point k_Y ~ N(k_X, σ). This is often referred to as the proposal distribution.
  3. Move to the candidate point with probability:  min( π(k_Y)/π(K_X), 1)
  4. Repeat.

The following code demonstrates this process in action for a simple normal target distribution.

################################################################
###     Metropolis-Hastings Visualization                #######
###      Created by Corey Chivers, 2012                #########
################################################################

mh_vis<-function(prop_sd=0.1,target_mu=0,
target_sd=1,seed=1,iter=5000,plot_file='MH.pdf')
{
plot_range=c(target_mu-3*target_sd,target_mu+3*target_sd)
track <- NULL
k_X = seed; ## set k_X to the seed position

pdf(plot_file)
par(mfrow=c(3,1),mgp = c(1, 0.5, 0))

for(i in 1:iter)
{
track<-c(track,k_X)    ## The chain
k_Y = rnorm(1,k_X,prop_sd) ## Candidate point

## -- plot kernal density estimation of the Chain
par(mar=c(0,3,2,3),xaxt='n',yaxt='n')

curve(dnorm(x,target_mu,target_sd),col='blue',lty=2,lwd=2,xlim=plot_range)
if(i > 2)
lines(density(track,adjust=1.5),col='red',lwd=2)

## -- plot the chain
par(mar=c(0,3,0,3))
plot(track,1:i,xlim=plot_range,main='',type='l',ylab='Trace')

pi_Y = dnorm(k_Y,target_mu,target_sd,log=TRUE)
pi_X = dnorm(k_X,target_mu,target_sd,log=TRUE)

## -- plot the target distribution and propsal distribution actions
par(mar=c(3,3,0,3),xaxt='s')
curve(dnorm(x,target_mu,target_sd),xlim=plot_range,col='blue',lty=2,ylab='Metropolis-Hastings',lwd=2)
curve(dnorm(x,k_X,prop_sd),col='black',add=TRUE)
abline(v=k_X,lwd=2)
points(k_Y,0,pch=19,cex=2)
abline(v=k_Y)

a_X_Y = (pi_Y)-(pi_X)
a_X_Y = a_X_Y

if (a_X_Y > 0)
a_X_Y = 0

## Accept move with a probability a_X_Y
if (log(runif(1))<=a_X_Y)
{
k_X = k_Y;
points(k_Y,0,pch=19,col='green',cex=2)
abline( v=k_X,col='black',lwd=2)
}
## Adapt the poposal
if(i>100)
prop_sd=sd(track[floor(i/2):i])

if(i%%100==0)
print(paste(i,'of',iter))
}
dev.off()
}

mh_vis()

A common problem in the implementation of this algorithm is the selection of σ. Efficient mixing (the rate at which the chain converges to the  target distribution) occurs when σ approximates the standard deviation of the target distribution. When we don’t know this value in advance. we can allow σ to adapt based on the history of the chain so far. In the above example, σ is simply updated to take the value of the standard deviation of some previous points in the chain.

The output is a multipage pdf which you can scroll through to animate the MCMC.

The top panel shows the target distribution (blue dotted) and a kernel smoothed estimate of the target via the MCMC samples. The second panel shows a trace of the chain, and the bottom panel illustrates the steps of the algorithm itself.

Note: notice the first 100 or so iterations were a rather poor representation of the target distribution. In practice, we would ‘burn’ the first n iterations of the chain – typically the first 100-1000.

Gauging Interest in a Montreal R User Group

By Posted in Probability, Rstats, Teaching Leave a comment

** UPDATE ** We’ve done it! Visit the Montreal R User Group site to join.

Some of us over at McGill’s Biology Graduate Student Association have been developing and delivering R/Statistics workshops over the last few years. Through invited graduate students and faculty, we have tackled  everything from multi-part introductory workshops to get your feet wet, to special topics such as GLMs, GAMs, Multi-model inference, Phylogenetic analysis, Bayesian modeling, Meta-analysis, Ordination, Programming and more.

We are currently toying with the idea of opening the workshop beyond the department, and even beyond McGill by founding a Montreal R User Group. If you are interested in attending and/or speaking at a Montreal R User Group, we’d love to hear from you! If there is enough interest, we’ll start up a group.

General Bayesian estimation using MHadaptive

By Posted in Probability, Rstats 9 Comments

If you can write the likelihood function for your model, MHadaptive will take care of the rest (ie. all that MCMC business). I wrote this R package to simplify the estimation of posterior distributions of arbitrary models. Here’s how it works:

1) Define your model (ie the likelihood * prior). In this example, lets build a simple linear regression model.

(log)Likelihood:

li_reg<-function(pars,data)
{
a<-pars[1]      #intercept
b<-pars[2]      #slope
sd_e<-pars[3]   #error (residuals)
if(sd_e<=0){return(NaN)}
pred <- a + b * data[,1]
log_likelihood<-sum( dnorm(data[,2],pred,sd_e, log=TRUE) )
prior<- prior_reg(pars)
return(log_likelihood + prior)
}

Prior:

prior_reg<-function(pars)
{
a<-pars[1]          #intercept
b<-pars[2]          #slope
epsilon<-pars[3]    #error

prior_a<-dnorm(a,0,100,log=TRUE)     ## non-informative (flat) priors on all
prior_b<-dnorm(b,0,100,log=TRUE)     ## parameters.
prior_epsilon<-dgamma(epsilon,1,1/100,log=TRUE)

return(prior_a + prior_b + prior_epsilon)
}

Now lets just simulate some data to give it a test run:

x<-runif(30,5,15)
y<-x+rnorm(30,0,5) ##Slope=1, intercept=0, epsilon=5
d<-cbind(x,y)
plot(x,y)

2) The function Metro_Hastings() does all the work. Just pass your model to this function, sit back and let MC Emmcee take it away.

mcmc_r<-Metro_Hastings(li_func=li_reg,pars=c(0,1,1),
par_names=c('a','b','epsilon'),data=d)

3) You can view the posteriors of all model parameters using plotMH()

plotMH(mcmc_r)

By default, this will also plot the pair-wise correlation between all parameters.

4) Print posterior Credible Intervals.

BCI(mcmc_r)
#              0.025    0.975
# a       -5.3345970 6.841016
# b        0.4216079 1.690075
# epsilon  3.8863393 6.660037

Tadda! Easy-Peasy.

For a more introductory look at Bayesian modeling, check out the slides and script file from an R workshop I gave at McGill on the subject. There are some additional optional arguments you can pass to Metro_Hastings() which you can read all about in the package manual. You can get the package source from cran, or from my github page.

*notes: MHadaptive is only recommended for relatively low dimensional models. Mixing can be quite slow for higher order models.

Monty Hall by simulation in R

By Posted in Probability, Rstats, Teaching Tagged , 17 Comments

(Almost) every introductory course in probability introduces conditional probability using the famous Monte Hall problem. In a nutshell, the problem is one of deciding on a best strategy in a simple game. In the game, the contestant is asked to select one of three doors. Behind one of the doors is a great prize (free attendance to an R workshop, lets say), and there is a bum prize behind each of the other two doors. The bum prize is usually depicted to be a goat, but I don’t think that would be such a bad prize, so let’s say that behind two of the doors is a bunch of poorly collected data for you to analyse. Once the contestant makes her first selection, the host then opens one of the other two doors to reveal one of the bum prizes.

At this point, the contestant is given the choice to either stay with her original selection, or switch to the other remaining unopened door. What should she do?

If you’re reading this blog, you no doubt gleefully shouted “Switch! Switch! Daddy needs a ticket to that R workshop!”. And you also, no doubt, can prove this to be the best strategy using the logic of probability. You reason that the contestant’s chance of selecting the winning door from the onset was 1/3, giving her a 2/3 probability of being wrong. Once one door with a bum prize has been opened, the contestant is now choosing between two doors. Knowing that there was only a 1/3 chance that original selection was correct, there is now a 2/3 chance that the alternate door is the winner.

As I have mentioned in previous posts, I have found that engaging students to think through logical reasoning problems can be greatly enhanced by appealing to their desire to see it in action. To that end, I whipped up this little script to simulate repeatedly playing the Monte Hall game.


#####################################################
# Simulation of the Monty Hall Problem
# Demonstrates that switching gives you better odds
# than staying with your initial guess
#
# Corey Chivers, 2012
#####################################################

rm(list=ls())
monty<-function(strat='stay',N=1000,print_games=TRUE)
{
 doors<-1:3 #initialize the doors behind one of which is a good prize
 win<-0 #to keep track of number of wins

for(i in 1:N)
 {
 prize<-floor(runif(1,1,4)) #randomize which door has the good prize
 guess<-floor(runif(1,1,4)) #guess a door at random

## Reveal one of the doors you didn't pick which has a bum prize
 if(prize!=guess)
 reveal<-doors[-c(prize,guess)]
 else
 reveal<-sample(doors[-c(prize,guess)],1)

 ## Stay with your initial guess or switch
 if(strat=='switch')
 select<-doors[-c(reveal,guess)]
 if(strat=='stay')
 select<-guess
 if(strat=='random')
 select<-sample(doors[-reveal],1)

## Count up your wins
 if(select==prize)
 {
 win<-win+1
 outcome<-'Winner!'
 }else
 outcome<-'Losser!'

if(print_games)
 cat(paste('Guess: ',guess,
 '\nRevealed: ',reveal,
 '\nSelection: ',select,
 '\nPrize door: ',prize,
 '\n',outcome,'\n\n',sep=''))
 }
 cat(paste('Using the ',strat,' strategy, your win percentage was ',win/N*100,'%\n',sep='')) #Print the win percentage of your strategy
}

Students can then use the function to simulate N games under the strategies ‘stay’, ‘switch’, and ‘random’. Invoking the function using:


monty(strat="stay")
monty(strat="switch")
monty(strat="random")

Hey, look at that – it is better to switch! Feel free to use this in your own class, and let me know if you use it or adapt it in an interesting way!

Edit: Thanks to Ken for pointing out that saying that ‘switching is always better’ is not quite right (you will loose 1/3 of the time, after all), but rather that switching is a rational best strategy, given your state of knowledge.

Uncertainty in markov chains: fun with snakes and ladders

By Posted in Probability, Rstats Tagged , , , 6 Comments

I love board games. Over the holidays, I came across this interesting post over at Arthur Charpentier’s Freakonometrics blog about the classic game of snakes and ladders. The post is a nice little demonstration of how the game can be formulated completely as a Markov chain, and can be analysed simply using the mathematics of state transitions.

The particular board which was analysed had the following ‘portals’:

 starting=c(4,9,17,20,28,40,51,54,62,64,63,71,93,95,99)
 ending=c(14,31,7,38,84,59,67,34,19,60,81,91,73,75,78)

Given that a player roles a six sided die to determine how many positions forward to travel, the transition matrix can be defined as:


n=100
 M=matrix(0,n+1,n+1+6) ## from n+1 starting positions (0-100 inclusive) to n+1+6 ending (includes overshooting the last position)
 rownames(M)=0:n
 colnames(M)=0:(n+6)

for(i in 1:6){diag(M[,(i+1):(i+1+n)])=1/6} ##dice role probs from each position on the board

M[,n+1]=apply(M[,(n+1):(n+1+6)],1,sum) ##collect all of the 'overshooting' the ending probabilities
 M=M[,1:(n+1)]

for(i in 1:length(starting))
 {
 v=M[,starting[i]+1]
 ind=which(v>0)
 M[ind,starting[i]+1]=0
 M[ind,ending[i]+1]=M[ind,ending[i]+1]+v[ind]
 }

In order to calculate the probability distribution of a player’s position after h rolls, the initial position vector (what state is currently occupied) is multiplied by the transition matrix raised to the hth power.

 ### Multiply the transition matrix to get the position distribution ###
powermat<-function(P,h){
Ph<-P
if(h>1)
{
for(k in 2:h)
{
Ph<-Ph%*%P
}
}
return(Ph)
}
### -- ###

initial<-c(1,rep(0,n))
initial%*%powermat(M,h=1)

You can vary h and get the probability distribution of where a player will be on the board after that many rolls. Neat!

The thing is, this got me wondering… For the first roll, a player can end up in 1 of 6 possible positions (for this board 1,2,3,14,5 or 6), each with a 1/6 chance. We therefore can predict the position of a player after one roll with a good degree of confidence. If we wanted to predict the player’s position at roll 3, however, there are more positions which are possible (though not equally likely). So we would probably be less confident when trying to predict the position of a player after 3 rolls, and we would feel less and less confident the further out we get.

However, the game does end (although unfortunately for those who would like to move on to video games, this is not guaranteed – I leave it to the reader to prove this) and therefore we might expect to be fairly confident in predicting a player’s position after 100 rolls (they are probably at the finish line, of course). Which begs the question, how many rolls into a game would you be the least confident in predicting a player’s position?

To answer this question, we need a measure of uncertainty which can quantify how well we could predict a player’s position. It turns out, that the Shannon entropy measure does just that! The formula is very simple:

H=-∑p log(p)

entropy<-function(p){
ind<-which(p>0)
return(-sum(p[ind]*log(p[ind])))
}

The Shannon entropy defines how much information is missing about the outcome of a random variable. So, if there is no information missing, we know the outcome with p=1, and the Shannon entropy = 0. If a random variable can have n possible outcomes, then the Shannon entropy is at a maximum when p=1/n for each.

So, back to my question: how many rolls into a game is our uncertainty about a player’s position on the board at a maximum? Keep in mind that we are talking about uncertainty with respect to our predictions before the game is started. Any knowledge of a player’s position at any point in the game would of course change our predictions and associated uncertainty. To answer this question, we just need to calculate the Shannon entropy of the outcome distribution generated by our Markov chain, and find at which point it is maximised.

##############################################################
############ Calculate the entropy after n turns #############
entropy<-function(p)
{
ind<-which(p>0)
return(-sum(p[ind]*log(p[ind])))
}

turns<-100
ent<-numeric(turns)
for(n in 1:turns)
ent[n]<-entropy(initial%*%powermat(M,n))

plot(ent,type='b',xlab='Turn',ylab='Entropy')

Which is at a maximum (highest uncertainty) at roll 10. We are most certain of a player’s position at roll 1 as we might expect, but again from rolls 33 and on. After which, we become increasingly certain that the player has reached the finish line.

TL;DR When predicting player positions in snakes and ladders, forecasts are least reliable ten rolls in. Have fun!

Visualizing Sampling Distributions

By Posted in Probability, Rstats, Teaching, Uncategorized Leave a comment

Teacher: “How variable is your estimate of the mean?”

Student: “Uhhh, it’s not. I took a sample and calculated the sample mean. I only have one number.”

Teacher: “Yes, but what is the standard deviation of sample means?”

Student: “What do you mean means, I only have the one friggin number.”

Statisticians have a habit of talking about single events as though they’ve happened (or could happen) over and over again.  This is the basis of the Frequentist paradigm, and I’ve found that it really irks early students of statistics. Questions of the type: “How variable is that estimate?” asked by a statistician translates to “How variable would our collection of estimates be if we were to draw samples of the same size from the population, over and over again?”

As a way to help students get into this way of thinking, I have found simulations to be quite useful.  Here is an R script to demonstrate the sampling distribution of means and how we can reproduce the theoretical standard error of the mean.


## This script plots a histogram of sample means from a known population and compares this
## distribution against the theoretical Standard Error of the Means distribution.

## You can play around with sample size (n) to see how the standard error distribution changes.

rm(list=ls())

var_ <- new.env()
n<-20            ## Sample n individuals at a time
p_mean<-0        ## Population mean
p_sd<-1            ## Population standard deviation
N<-500            ## Number of times the experiment (sampling) is replicated

pdf('SE.pdf')

for(i in 1:N)                                ## do the experiment N times
{
smp<-rnorm(n,p_mean,p_sd)                 ## sample n data points from the population

var_$x_bar<-c(var_$x_bar,mean(smp))         ## keep track of the mean (x_bar) from each sample

hist(var_$x_bar,probability=TRUE,col="red",xlim=c(-4,4),xlab="x / x_bar",main="",ylim=c(0,2.2))  # Plot a histogram of x_bar values
points(mean(smp),0,pch=19,cex=1.5,col='black')
curve(dnorm(x,p_mean,p_sd/sqrt(n)),lwd=3,add=TRUE)

text(2.5,1.75,labels=paste('sd/sqrt(n) = ',round(p_sd/sqrt(n),2),sep=''))
text(2.5,1.5,labels=paste('standard deviation of\nsample means = ',round(sd(var_$x_bar),2),sep='') )

curve(dnorm(x,p_mean,p_sd),main="",ylab="",xlim=c(-4,4),xlab="X",col="blue",lwd=3,add=TRUE) ## Plot the sample

text(2.5,0.5,labels=paste('# of means drawn = ',i,sep=''))
text(2.5,0.35,labels=paste('Sample size (n) = ',n,sep=''))
points(smp,rep(0,n),pch=19,cex=1.5,col='purple')
abline(v= mean(smp),col='purple',lwd=4)

legend("topleft",legend=c('Sample points','Population Distribution','Sample mean','Theoretical SE','Empirical SE'),
lty=c(0,1,1,1,1,1,1),lwd=c(0,3,3,3,3,3,3),pch=c(16,NA,NA,NA,NA,NA,NA),col=c('purple','blue','purple','black','red'))

print(paste(i," of ",N))
}
dev.off()

############################################################################################
############################################################################################

The output of the script is a multi-page pdf which can be flipped through to show the building of a histogram of sample means converging on the theoretical sampling distribution.


Visualizing Bayesian Updating

By Posted in Probability, Rstats, Teaching, Uncategorized Tagged , , 5 Comments

One of the most straightforward examples of how we use Bayes to update our beliefs as we acquire more information can be seen with a simple Bernoulli process. That is, a process which has only two  possible outcomes.

Probably the most commonly thought of example is that of a coin toss. The outcome of tossing a coin can only be either heads, or tails (barring the case that the coin lands perfectly on edge), but there are many other real world examples of Bernoulli processes. In manufacturing, a widget may come off of the production line either working, or faulty.  We may wish to know the probability that a given widget will be faulty.  We can solve this using Bayesian updating.

I’ve put together this little piece of R code to help visualize how our beliefs about the probability of success (heads, functioning widget, etc) are updated as we observe more and more outcomes.


## Simulate Bayesian Binomial updating

sim_bayes<-function(p=0.5,N=10,y_lim=15)
{
  success<-0
  curve(dbeta(x,1,1),xlim=c(0,1),ylim=c(0,y_lim),xlab='p',ylab='Posterior Density',lty=2)
  legend('topright',legend=c('Prior','Updated Posteriors','Final Posterior'),lty=c(2,1,1),col=c('black','black','red'))
  for(i in 1:N)
  {
    if(runif(1,0,1)<=p)
        success<-success+1

    curve(dbeta(x,success+1,(i-success)+1),add=TRUE)
    print(paste(success,"successes and ",i-success," failures"))
  }
  curve(dbeta(x,success+1,(i-success)+1),add=TRUE,col='red',lwd=1.5)
}

sim_bayes(p=0.6,N=90)

The result is a plot of posterior (which become the new prior) distributions as we make more and more observations from a Bernoulli process.

With each new observation, the posterior distribution is updated according to Bayes rule. You can change p to see how belief changes for low, or high probability outcomes, and N for to see how belief about p asymptotes to the true value after many observations.

P-value fallacy on More or Less

By Posted in Probability, Uncategorized 23 Comments

The excellent BBC podcast More or Less does a great job at communicating and demystifying statistics in the news to a general audience. While listening to the most recent episode (Is Salt Bad for You? 19 Aug 2011), I was pleased to hear the host offer a clear, albeit incomplete, explanation of p-values, as reported in scientific studies like the ones being discussed in the episode. I was disappointed, however, to hear him go on to forward an all too common fallacious extension of their interpretation. I count the show’s host, Tim Harford, among the best when it comes to statistical interpretation, and really feel that his work has improved public understanding, but it would appear that even the best of us can fall victim to this little trap.

The trap:

When conducting Frequentist null hypothesis significance testing, the p-value represents the probability that we would observe a result as extreme or more (this was left out of the loose definition in the podcast) than our result IF the null hypothesis were true.  So, obtaining a very small p-value implies that our result is very unlikely under the null hypothesis.  From this, our logic extends to the decision statement:

“If the data is unlikely under the null hypothesis, then either we observed a low probability event, or it must be that the null hypothesis is not true.”

It is important to note that only one of these options can be correct.  The p-value tells us something about the likelihood of the data, in a world where the null hypothesis is true.  If we choose to believe the first option, the p-value has direct meaning as per the definition above.  However, if we choose to believe the second option (which is traditionally done when p<0.05), we now believe in a world where the null hypothesis is not true.  The p-value is never a statement about the probability of hypotheses, but rather is a statement about data under hypothetical assumptions. Since the p-value is a statement about data when the null is true, it cannot be a statement about the data when the null is not true.

How does this pertain to what was said  in the episode?  The host stated that:

“…you could be 93% confident that the results didn’t happen by chance, and still not reach statistical significance.”

Referring to the case where you have observed a p-value of 0.07.  The implication is that you would have 1-p=0.93 probability that the null is not true (ie that your observations are not the result of chance alone).  From the discussion above, we can begin to see why this cannot be the case.  The p-value is a statement about your results only when the null hypothesis is true, and therefor cannot be a statement about the probability that it is false!

An example:

With our complete definition of the p-value in mind, lets look at an example. Consider a hypothetical study similar to those analyzed by the Cochrane group, in which a thousand or so individuals participated. In this hypothetical study, you observe no mean difference in mortality between the high salt and low salt groups. Such a result would lead to a p-value of 0.5, or 50%. Meaning that if there is no real effect, there is a 50% chance that you would observe a result greater than zero, however slightly. Using the incorrect logic, you would say:

“I am 50% confident that the results are not due to chance.”

Or, in other words, that there is a 50% probability that there is some adverse effect of salt. This may seem reasonable at first blush, however, consider now another hypothetical study in which you have recruited just about every adult in the population, (maybe you’re giving away iPads or something), and again you observe zero mean difference in mortality between groups. You would once again have a p-value of 0.5, and might again erroneously state that you are 50% confident that there is an effect. After some thought, however, you would conclude that the second study provided you with more confidence about whether or not there is any effect than did the first, by virtue of having measured so many people, and yet your erroneous interpretation of the p-value tells you that your confidence is the same.

The solution:

I have heard this fallacious interpretation of p-values everywhere from my undergraduate Biometry students, to highly reputable peer reviewed research publications.  Why is this error so prevalent?  It seems to me that the issue lies in the fact that what we really want to be able to say is not a statement about our results under the assumption of no effect (the p-value), but rather a statement about hypotheses given our results (which we do not get directly through the p-value).

One solution to this problem lies in a statistical concept known as power. Power is the calculation of how likely it is that you would observe a p-value below some critical value (usually the canonical 0.05), for both a given sample size and the size of the effect that you wish to detect. The smaller the size of the real effect that you wish to measure, the higher the sample size required if you want to have a high probability of finding statistical significance.

This is why it is important to distinguish, as was done in the episode, between statistical significance, and biological, or practical significance. A study may have high power, due to a large sample size, and this can lead to statistically significant results, even for very small biological effects. Alternatively the study may have low power, in which case it may not find statistically significant results, even if there is indeed some real biologically relevant effect present.

Another solution is to switch to a Bayesian perspective.  Bayesian methods allow us to make direct statements about what we are really interested in – namely, the probability that there is some effect (general hypotheses), as well as the probability of the strength of that effect (specific hypotheses).

In short:

What we really want is the probability of hypotheses given our data (written as P(H | D) ), which we can obtain by applying Bayes rule.

What we get from a p-value is the probability of observing something as extreme or more than our data, under the null hypothesis ( written as P(x>=D | Ho) ).  Isn’t that awkward? No wonder it is so commonly misrepresented.

So, my word of caution is this: We have to remember that the p-value is only a statement of the likelihood of making an observation as extreme or more than your observation, if there is, in fact, no real effect present. We must be careful not to perform the tempting, but erroneous, logical inversion of using it to represent the probability that a hypothesis is, or is not true. An easy little catch phrase to remember this is:

“A lack of evidence for something is not a stack of evidence against it.”

Using simulation to demonstrate theory: Hardy-Weinberg Equilibrium

By Posted in Probability, Rstats, Teaching 15 Comments

One of my teaching roles is in an introductory Genetics course, where first year students are presented with a wide range of new ideas at a relatively fast pace.  It seems that often, students choose to take a memorization approach to learning the material, rather than taking the chance to think about how and why these genetic concepts actually work.  It is my conviction that, as teachers, it is our role to provide students with the opportunities to engage with the course material, and construct a solid understanding that will serve them as they proceed on to higher specialization.

When it comes to bang for my pedagogical buck, I have found that you really can’t beat the use of simulation as a platform for providing the opportunity for students to engage with theoretical concepts.  Here is an R script which I have written and used to allow students to explore how random mating in a population leads to the well known Hardy-Weinberg (HW) distribution.

For those who need a refresher, HW describes the genotype frequencies in randomly mating population. For the simple two allele case (A >> a), the frequencies are denoted by p and q; freq(A) = p; freq(a) = q; p + q = 1. If the population is in equilibrium, then freq(AA) = p2 for the AA homozygotes in the population, freq(aa) = q2 for the aa homozygotes, and freq(Aa) = 2pq for the heterozygotes.

What doesn’t usually get mentioned in introductory courses, is that the HW formula provides the expected frequencies of each genotype.  Of course, in real, finite populations, there will be variability around these values.  The seeming exactness of HW obscures the random processes at play.  To help students see how HW arises in finite populations (as opposed to the theoretical infinite populations required for the strict solution), I let them play with this simulation (R script).

Students can play around with the population size (N) and the number of generations (num_generations), to see how well the simulated populations correspond to the predicted HW.  Here is a plot of 200 simulated populations of size N=200, which are initiated out of the HW equilibrium and then randomly mated for one generation:

Feel free to try it out in your own class!

-BayesianBiologist